PPO算法：Proximal Policy Optimization

Posted Sep 1, 2025 Updated Sep 28, 2025

By quantux

8 min read

一、引言

PPO的特点:
PPO 采用了代理目标函数（surrogate object function），一个样本可以经历多个 epoch 的小批量更新，而常规的 Policy Gradient 算法每个数据样本只进行一次梯度更新。它具备 TRPO 的优点，同时更简单，样本复杂度也更优。

其他算法的不足:

Q-learning：在许多简单问题上表现不佳，且其原理尚未被充分理解。
Vanilla PG：数据效率低，鲁棒性差。
TRPO：较为复杂，与包含噪声或参数共享的架构不兼容。

二、相关算法目标函数

2.1 Policy Gradient Methods

目标奖励函数为：

\[L^{PG}(\theta)=\hat{\mathbb{E}}[log \pi_{\theta}(a_{t} | s_{t}) \hat{A}_{t}]\]

其中，$\hat{A}_{t}$是时间步t处优势函数的估计量，$\hat{A}_{t}=q(a_{t}, s_{t})-b(s_{t})$。

需要注意的是，使用相同的轨迹对这个损失 $L^{PG}$ 进行多步优化虽然很有吸引力，但缺乏理论证明，而且在实际中常常会导致破坏性的大幅策略更新。

2.2 TRPO

目标奖励函数为：

\[\underset{\theta}{maxmize} \hat{\mathbb{E}}[\frac{\pi_{\theta}(a_{t} | s_{t})}{\pi_{\theta_{old }}(a_{t} | s_{t})} \hat{A}_{t}]\]

约束条件：

\[s.t. \hat{\mathbb{E}}_{t}[K L[\pi_{\theta_{old }}(* | s_{t}), \pi_{\theta_{old }}(* | s_{t})]] \leq \delta\]

因此，TRPO 本质上求解的是以下最优化问题：

\[\underset{\theta}{maxmize} \hat{\mathbb{E}}[\frac{\pi_{\theta}(a_{t} | s_{t})}{\pi_{old }(a_{t} | s_{t})} \hat{A}_{t}-\beta K L[\pi_{old }(a_{t} | s_{t}), \pi_{\theta}(a_{t} | s_{t})]]\]

TRPO 使用硬约束而非将约束带入优化目标作为惩罚项，原因是难以找到单一固定的惩罚系数$\beta$。

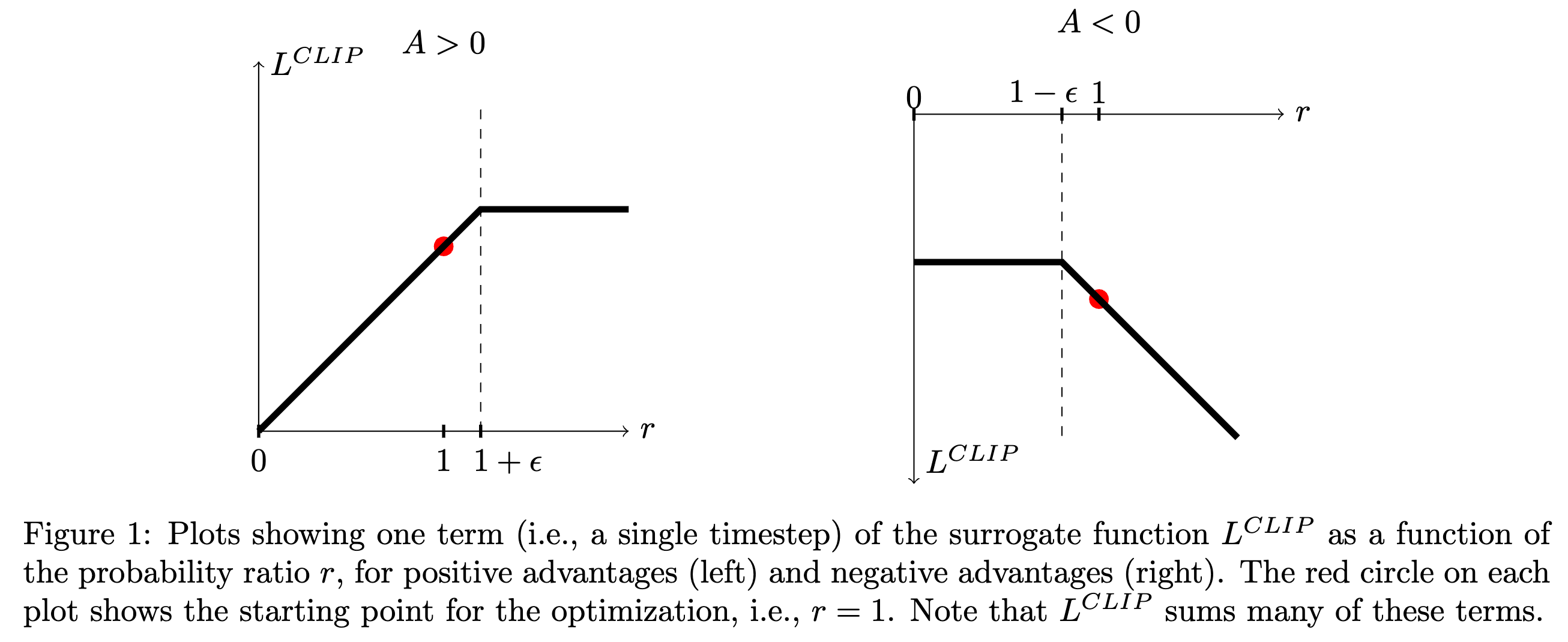
三、PPO 1：Clipped Surrogate Objective

重要性采样系数$r_{t}(\theta)=\cfrac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}$某种程度上也可以衡量新旧策略之间的差异程度。对于初始策略$r_{old}(\theta)=1$。

\[L^{CPI}(\theta)=\hat{\mathbb{E}}[\frac{\pi_{\theta}(a_{t} | s_{t})}{\pi_{\theta_{old }}(a_{t} | s_{t})} \hat{A}_{t}]=\hat{\mathbb{E}}[r_{t}(\theta) \hat{A}_{t}]\]

这是 TRPO 最大化的代理目标函数（CPI：conservative policy iteration）。

直接优化上述目标会导致很大幅度的策略更新，因此需要对策略更新的幅度（$r_{t}(\theta)$ 偏离 1 的程度）进行惩罚。

PPO 代理目标函数

\[L^{C L I P}(\theta)=\hat{\mathbb{E}}[min(r_{t}(\theta) \hat{A}_{t}, clip(r_{t}(\theta), 1-\epsilon, 1+\epsilon) \hat{A}_{t})].\]

第一项$r_{t}(\theta) \hat{A}_{t}$ 就是 $L^{CPI}$。
第二项$clip(r_{t}(\theta), 1-\epsilon, 1+\epsilon) \hat{A}_{t}$ 是截断目标，消除了将$r_{t}$移到区间$[1-\epsilon, 1+\epsilon]$之外的动机。
最终的目标取第一项和第二项的最小值，所以最终目标是未截断目标的一个下界（悲观界）。

如果没有约束条件，最大化$L^{CPI}$将会导致过大的策略更新，因此需要考虑修改上述目标函数，以惩罚使$r_{t}(\theta)$远离1的策略变化。

不同情况下的取值

$A_t$	$0< r_t< \infty$	$clip$	$min(r_tA_t, clip)$
+	$1+\epsilon < r_t< +\infty$	$1+\epsilon$	$(1+\epsilon)\times A_t$
+	$1-\epsilon < r_t < 1+\epsilon$	$r_t$	$r_t\times A_t$
+	$0< r_t < 1-\epsilon$	$1-\epsilon$	$r_t\times A_t$
-	$1+\epsilon < r_t < +\infty$	$1+\epsilon$	$r_t\times A_t$
-	$1-\epsilon < r_t < 1+\epsilon$	$r_t$	$r_t\times A_t$
-	$0 < r_t <1-\epsilon$	$1-\epsilon$	$(1-\epsilon)\times A_t$

策略更新对比

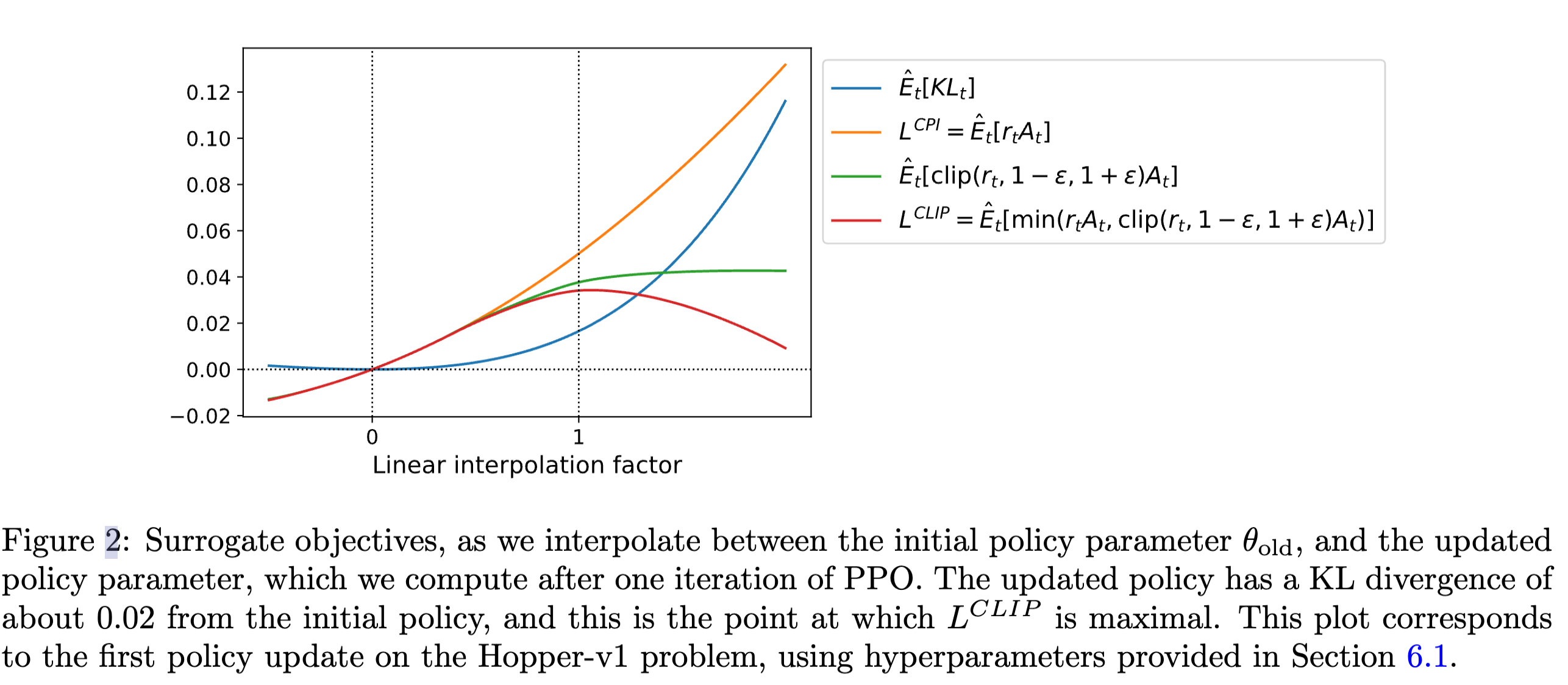
在 PPO 论文的 Figure2 中，线性插值因子是理解代理目标函数$L^{CLIP}$与原始目标$L^{CPI}$关系的关键。该实验基于连续控制问题，通过策略更新方向的线性插值（即从旧策略$\theta_{old }$ 到新策略$\theta_{new }$的插值），展示了多个目标函数的变化趋势。

插值公式：设插值因子为$\epsilon \in[0,1]$，中间策略为$\theta_{\epsilon} = \theta_{\text{old}} + \epsilon (\theta_{\text{new}} - \theta_{\text{old}})$
当$\epsilon=0$时，策略为旧策略；
当$\epsilon=1$时，策略为新策略；中间值表示不同幅度的策略更新。

目标函数对比：实验对比了$L^{CLIP}$（裁剪后的代理目标）与$L^{CPI}$（保守策略迭代的原始目标），以及可能的其他目标（如 KL 散度、奖励函数等）。

四、PPO 2：Adaptive KL Penalty Coefficient β

这种形式将 KL 散度约束作为惩罚项放到目标函数中，同时自适应调节 KL 项惩罚系数$\beta$，目标函数为：

\[L^{KLPEN}(\theta) = \hat{\mathbb{E}}[\cfrac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}\hat{A}_t] - \beta KL[\pi_{old}(\cdot|s_t), \pi_{\theta}(\cdot|s_t))]\]

同时，根据KL散度取值自适应调节：

\[d=\mathbb{\hat{E}}_{t}[KL[\pi_{old}(\cdot|s_{t}), \pi_{\theta}(\cdot|s_{t})]]\]

若 $d<d_{tar } / 1.5$，则$\beta \leftarrow \beta / 2$
若 $d>d_{tar} \times 1.5$，则$\beta \leftarrow \beta \times 2$

五、Actor和Critic共享参数架构

很多算法为了降低优势函数的估计误差都会学习状态值函数 $v(s)$，因此可以使用 actor 和 critic 共享的架构，例如：

High-Dimensional Continuous Control Using Generalized Advantage Estimation
Asynchronous Methods for Deep Reinforcement Learning

六、GAE: General Advantage Estimation

High-Dimensional Continuous Control Using Generalized Advantage Estimation
https://arxiv.org/pdf/1506.02438

针对策略梯度（Policy Gradient）算法存在的两个主要问题突出的解决方案：

问题：
样本效率低
在训练样本数据不断变化的情况下如何稳定得获得策略提升？ 方法：
GAE
TRPO

考虑一个undiscounted（$\gamma=1$）形式的MDP策略优化问题，策略梯度算法通过最大化累计奖励期望值来进行策略提升： $g :=\nabla_{\theta}\mathbb{E}[\sum_{t=0}^{\infty}r_t] = \mathbb{E}[\sum_{t=0}^{\infty}\Psi_t\nabla_{\theta}log\pi_{\theta}(a_t|s_t)]$ 其中$\Psi_t$有以下几种形式：

$\sum_{t=0}^{\infty}r_t$：轨迹的累计奖励
$\sum_{t=t’}^{\infty}r_t$：执行动作$a_{t’}$之后的累计奖励（rewards to go）
$\sum_{t=t’}^{\infty}r_t - b(s_t)$：减去baseline
$Q^{\pi}(s_t,a_t)$：动作价值函数
$A^{\pi}(s_t,a_t)=Q^{\pi}(s_t,a_t)-V^{\pi}(s_t)$：优势函数
$\delta_t = r_t + \gamma v(s_{t+1}) - v(s_t)$：TD Error

动作价值函数： $Q^{\pi}(s_t,a_t)=\mathbb{E}_{s_{t+1}:\infty,a_{t+1}:\infty}\sum_{l=0}^{\infty}r_{t+l}$

状态价值函数： $V^{\pi}(s_t)=\mathbb{E}_{s_{t+1}:\infty,a_t:\infty}\sum_{l=0}^{\infty}r_{t+l}$

TD Error： $\delta_t=r_t + \gamma v(s_{t+1}) - v(s_t)$ $\delta_{t+1}=r_{t+1} + \gamma v(s_{t+2}) - v(s_{t+1})$

优势函数的估计

针对优势函数进行策略梯度估计：

\[\hat{g}=\cfrac{1}{N}\sum_{n=t}^{N}\sum_{t=0}^{\infty}\hat{A_t^n}\nabla_{\theta}log\pi(a_t^n|s_t^n)\] \[\hat{A}_t^{(1)}:=\delta_t^V=-V(s_t)+r_t+\gamma V(s_{t+1})\] \[\hat{A}_t^{(2)}:=\delta_t^V + \gamma\delta_{t+1}^V=-V(s_t)+r_t+\gamma r_{t+1}+\gamma{^2} V(s_{t+2})\] \[\hat{A}_t^{(3)}:=\delta_t^V+ \gamma\delta_{t+1}^V + {\gamma}^2\delta_{t+2}^V=-V(s_t)+r_t+\gamma r_{t+1}+\gamma{^2} r_{t+2}+\gamma{^3} V(s_{t+3})\] \[...\] \[\hat{A}_t^{(k)}:=\sum_{t=0}^{k-1}\gamma^{l}\delta_{t+l}^V=-V(s_t)+r_t+\gamma r_{t+1}+\gamma{^2} r_{t+2}+...+\gamma{^k} V(s_{t+k})\] \[\hat{A}_t^{(\infty)}:=\sum_{t=0}^{\infty}\gamma^{l}\delta_{t+l}^V=-V(s_t)+\sum_{l=0}^{\infty}\gamma^{l}r_{t+l}\]

GAE定义为： $\begin{align} \hat{A}_t^{GAE(\gamma, \lambda)} &:=(1-\lambda)(\hat{A}_t^{(1)}+\lambda\hat{A}_t^{(2)}+\lambda^2\hat{A}_t^{(3)}+...)\\ &:=\sum_{l=0}^{\infty}(\gamma\lambda)^l\delta_{t+1}^V \end{align}$

$\gamma$和$\lambda$的作用都是平衡优势函数估计的偏差和方差：
当$\lambda=0$的时GAE估计低方差高偏差 $GAE(\gamma, 0) = r_t + \gamma V(s_{t+1}) -V(s_t)$
当$\lambda=1$的时GAE低偏差高方差 $GAE(\gamma, 1) = \sum_{l=0}^{\infty}\gamma ^{l}r_{t+l}-V(s_t)$
$\gamma$主要决定了scale of the value function $V^{\pi, \gamma}$，引入$\gamma<1$会给策略梯度的估计带来bias

This post is licensed under CC BY 4.0 by the author.