强化学习之蒙特卡洛方法

1. Monte Carlo Prediction

• First-visit MC
• Every-visit MC

使用蒙特卡洛估计的方法预估的样本必须满足独立同分布条件

It is worth mentioning that the samples used for mean estimation must be independent and identically distributed.

3个Monte Carlo Reinforcement Learning Algorithms:

• MC basic
• MC exploring starts
• MC e-Greedy : Learning without exploring starts

2. Monte Carlo Estimation of Action values

The policy evaluation problem for action values is to estimate q(s, a), the expected return when starting in state s, taking action a, and thereafter following policy ⇡.

==solutions==

• exploring starts：One way to do this is by specifying that the episodes start in a state–action pair, and that every pair has a nonzero probability of being selected as the start.
• to consider only policies that are stochastic with a nonzero probability of selecting all actions in each state

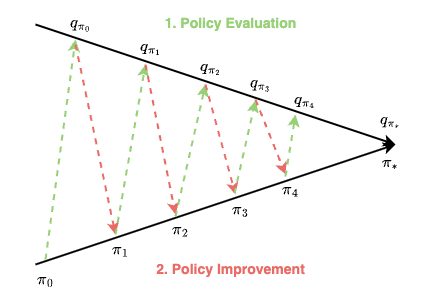
3. Monte Carlo control

==Monte Carlo Control：to approximate optimal policies==

Monte Carlo Basic: a model-free variant of policy iteration

• Policy Evaluation: estimate q(s,a) witch sufficiently many episodes starting from (s, a)
• Policy Improvement: greedy policy

Initialize: 
	pi: random policy

for k in PolicyIteration epoch, do:
	current policy pi: k
	for s in state space, do:

		Policy Evaluation:
		for a in action space, do:
			Collect sufficiently many episodes starting from (s,a) by following policy pi
			estimate q(s,a) with MC under policy pi

		Policy Improvement:
		a* = argmax q(s,a)
		pi(s,a) = 1 if a = a* else 0

==关键设计==

• initial visit
• first visit
• MC Basic is convergent when given sufficient samples.
• simple but low sample efficiency
• help to grasp the core idea of MC-based reinforcement learning

episode length greatly impacts the final optimal policy.

如果episode太短就无法学习到最优的optimal value和policy，因为episode too short to reach the target or get positive rewards。随着episode增大，距离target近的state首先获得nonzero values。

While the above analysis suggests that each episode must be sufficiently long, the episodes are not necessarily infinitely long.

稀疏奖励：

sparse reward: The sparse reward setting requires long episodes that can reach the target. This requirement is challenging to satisfy when the state space is large

solution: 设计非稀疏奖励

---

Monte Carlo Exploring Starts

相比于MC Basic有两个方面的提升：

1. utilize samples more efficiently：就样本使用效率而言，every visit效率最高，但是带来的问题是样本之间相互关联性越强。
   • ==initial visit==: 一个episode只用来估计初始<state, action>的value
   • ==first visit==: only count the first-time visit
   • ==every visit==: count every visit of a <state, action> pair
2. update policy more efficiently：when to update the policy
   • 收集所有$s_0$出发的action，然后更新$s_0$的策略
   • ==episode-by-episode==：收集一个episode之后就更新$s_0$的策略, Generalized Policy Iteration——数据有限，依然更新策略。

Initialize: 
	pi: random policy
	for k in PolicyIteration, do:
		current policy pi: k
		Episode Generation :starting from random <s,a> to ensure Exploring Starts following the current policy pi.

		for each step t in [T-1, T-2, ..., 0], do:
			Policy Evaluation (every visit):
				update every q(s,a) in the episode
			Policy Improvement (episode-by-episode):
				a* = argmax q(s,a)
				pi(s,a) = 1 if a = a* else 0

==关键设计==

• every-visit policy evaluation
• episode-by-episode policy improvement
• MC Basic和MC Exploring Starts都依赖于对每个<s,a>的充分探索

  However, this condition is difficult to meet in many applications, especially those involving physical interactions with environments. Can we remove the exploring starts requirement? The answer is MC e-Greedy.

It is easy to see that Monte Carlo ES cannot converge to any suboptimal policy. If it did, then the value function would eventually converge to the value function for that policy, and that in turn would cause the policy to change

Monte Carlo e-Greedy: Monte Carlo Control without Exploring Starts

如何避免exploring starts的前提？

确保所有动作被无限次选择的唯一通用方法，是智能体持续主动地选择这些动作。它强调了在强化学习中，探索（Exploration）的自主性和持续性是保证充分探索的必要条件。

soft policy: has a positive probability of taking any action at any state.

The only general way to ensure that all actions are selected infinitely often is for the agent to continue to select them.

主动探索：

• e-Greedy
• 玻尔兹曼探索
• 计数奖励

Initialize:
	pi: random policy

	for k in PolicyIteration, do:
		policy pi: k
		Episode Generation :starting from random <s,a> to ensure Exploring Starts following the current policy pi.

		for each step t in [T-1, T-2, ..., 0], do:
			Policy Evaluation (every visit):
				update every q(s,a) in the episode
			Policy Improvement (episode-by-episode):
				a* = argmax q(s,a)
				pi(s,a) = 1 - e*(N-1)/N if a = a* else e/N

==关键设计==

• Policy Improvement：e-Greedy 替换Greedy策略

4. summary

MC Basic, MC Exploring Starts, MC e-Greedy的区别和联系？

• MC Basic是蒙特卡洛强化学习方法的基础，后续很多算法都可以视为它的变种。
• MC Exploring Starts从提升样本效率（every-visit）和策略更新效率（episode-by-episode）两个方面优化MC-basic。
• MC e-Greedy相比于前两个算法，移除了对于exploring starts的要求。

5. 参考文档

Reinforcement Learning: An Introduction: chapter 5: http://incompleteideas.net/book/RLbook2020.pdf

Mathematical Foundation of RL: Monte Carlo Method